1. 우선순위 큐란?
•
정의
◦
우선순위가 높은 것을 가장 먼저 꺼내기 위해 만들어진 자료구조, 즉 우선순의의 개념을 큐에 도입한 자료 구조다.
◦
일반적으로 어떠한 자료구조를 명시하는 것이 아니고 추상적인 자료구조로 Heap을 사용해서 구현한다.
◦
데이터들이 우선순위를 가지고 있고 우선순위가 높은 데이터가 먼저 제거된다.
자료구조 | 삭제되는 요소 |
스택 | 가장 마지막에 들어온 데이터 |
큐 | 가장 처음에 들어온 데이터 |
우선순위 큐 | 가장 우선순위가 높은 데이터 |
◦
숫자가 클수록 우선순위가 높으면 최대힙, 낮을수록 우선순위가 높으면 최소힙이라 부른다.
•
사례
◦
시뮬레이션 시스템
◦
네트워크 트래픽 제어
◦
운영체제에서의 작업 스케쥴링
◦
수치 해석적인 계산
•
구현
◦
우선순위 큐는 배열, 연결리스트, 힙으로 구현 가능하다. 이 중에서 힙으로 구현하는 것이 가장 효율적이다.
구현 | 삽입 시 시간복잡도 | 추출 시 시간복잡도 | 설명 |
정렬된 배열 | O(n) | O(1) | 삽입 시 비교하며 삽입, 추출은 단순 추출 |
정렬된 리스트 | O(n) | O(1) | 삽입 시 비교하며 삽입, 추출은 단순 추출 |
힙 | O(logn) | O(logn) | 삽입 / 추출 시 기존 정렬 상태 유지 |
•
힙이란
◦
정의
▪
완전 이진 트리의 일종으로 우선순위 큐를 위해 만들어진 자료구조다.
▪
여러 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조다.
▪
반정렬 상태를 유지한다. 큰 값이 상위 레벨에 있고 작은 값이 하위에 있다 정도로만 정렬된다
•
간단하게 부모 노드의 값이 자식 노드의 값보다 항상 크거나 작은 이진 트리를 말한다.
⇒ 트리 구조로는 정렬되어있으나 배열에 저장된 형태는 정렬되어있지 않은것처럼 보임
◦
구현
▪
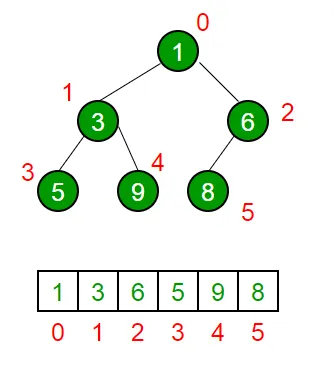
힙을 저장하는 표준적인 자료구조는 배열이다.
▪
구현을 쉽게 하기 위해 배열의 첫 번째 인덱스 0은 사용하지 않는다.
▪
특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.
•
ex) 루트 노드의 오른쪽 노드의 인덱스는 항상 3이다.
▪
힙에서의 부모 노드와 자식 노드의 관계는 다음과 같다.
•
왼쪽 자식의 인덱스 = 부모 인덱스 * 2
•
오른쪽 자식의 인덱스 = 부모 인덱스 * 2 + 1
•
부모의 인덱스 = 자식 인덱스 / 2
◦
삽입
▪
힙에 새로운 요소가 들어오면 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
▪
새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.
◦
삭제
▪
최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제된다.
•
최대 힙에서 삭제 연산은 최댓값을 가진 노드를 삭제하는 것이다.
▪
삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
▪
힙을 재구성한다.
Quere vs 우선순위 Queue
•
Queue 자료구조는 시간 순서상 가장 먼저 집어 넣은 데이터가 먼저 나오는 선입선출 구조이나 우선순위 큐는 들어간 순서에 상관없이 우선순위가 가장 높은 데이터가 먼저 나옵니다
•
우선순위 큐는 push, pop 모두 O(logn)
•
Heap은 우선순위 큐의 구현과 일치, 완전이진트리 구조로 보통 Array로 구현, 새로운 node를 Heap의 마지막 위치에 추가해야하는데 ,이 때 array 기반으로 구현해야 이 과정이 수월해지기 때문
◦
n번 째 node의 left child node = 2n
◦
n번 째 node의 right child node = 2n + 1
◦
n번 째 node의 parent node = n / 2