•
정의
◦
비선형 자료구조로 노드, 정점 그리고 엣지로 구성된 자료구조를 의미한다.
◦
그래프에서 등장하는 점을 Vertex 또는 Node라고 하며 두 노드 사이를 연결하는 것을 Edge라고 한다.
◦
인접성을 나타내는 것은 Degree라고 한다. 즉 해당 정점에 연결된 것이 몇 개인지 나타낸다.
▪
그래프의 분지수는 해당 그래프에서 가장 큰 분지수를 가지는 정점의 분지수이다.
◦
각 정점을 거쳐 이동하는 과정들을 경로라고 한다. 다만 같은 노드를 두 번 지나는 것은 경로로 치지 않는다.
◦
사이클은 특정 노드에서 출발하여 해당 노드로 돌아오는 것, 사이클이 없는 그래프는 트리, 사이클이 존재하지 않는다는 것은 특정 두 노드 간의 패스가 하나라는 것
•
특징
◦
그래프는 방향이 있을수도 없을 수도 있다.
▪
존재하는 경우 Directed, 존재하지 않는 경우 Undirected라고 한다.
◦
새로운 요소들의 추가/삭제가 용이하고 효율적이다.
▪
다양한 구조로 설계된다. 구조에 따라서 시간복잡도가 달라지고 다양하게 응용 가능하다.
•
Graph 표현법은 인접성을 나타내는 것
•
엣지에 방향성이 없는 경우, 양방향성을 가지므로 무방향 그래프라고 부름
•
엣지에 방향성을 표시하는 경우, 방향 그래프라고 부름
1.
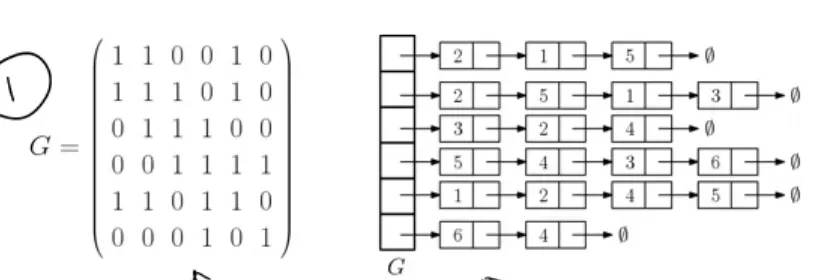
인접 행렬
•
정점의 갯수를 N이라 할 때, N x N 행렬을 생성, 엣지가 존재하는 부분을 1, 존재하지 않는 부분을 0로 처리한다.
•
이 경우, 엣지가 존재하지 않음을 행렬에 명시해야 하기 때문에 불필요한 메모리 낭비가 발생한다.
•
가중치 표현 시 인접 행렬은 각 행과 열에 1 대신 가중치를 표현한다.
2.
인접 리스트
•
각 노드에서 엣지가 있는 부분을 표시한다. 이때 총 엣지가 7개라면 총 14개의 리스트가 연결됨
•
가중치 표현 시 인접 리스트는 노드에 가중치 값을 추가하여 표현한다.
◦
시간복잡도/공간복잡도를 이야기할 땐, 노드, 정점, 엣지를 사용하여 표현한다.
◦
그래프에서 등장하는 점을 Vertex 또는 Node라고 하며 두 노드 사이를 연결하는 것을 Edge라고 한다.
◦
인접성을 나타내는 것은 Degree라고 한다. 즉 해당 정점에 연결된 것이 몇 개인지 나타낸다.
▪
그래프의 분지수는 해당 그래프에서 가장 큰 분지수를 가지는 정점의 분지수이다.
◦
각 정점을 거쳐 이동하는 과정들을 경로라고 한다. 다만 같은 노드를 두 번 지나는 것은 경로로 치지 않는다.
◦
사이클은 특정 노드에서 출발하여 해당 노드로 돌아오는 것, 사이클이 없는 그래프는 트리, 사이클이 존재하지 않는다는 것은 특정 두 노드 간의 패스가 하나라는 것
•
시간복잡도
◦
두 노드의 연결을 확인하는 연산
▪
인접 행렬의 경우, 고유 인덱스로 바로 접근가능하므로 O(1)의 시간복잡도를 가진다.
▪
인접 리스트의 경우, 한 노드의 인접 리스트 안에 특정 노드가 존재하는 지 확인해야 하므로 최악의 경우 O(N 또는 V)의 시간복잡도를 가진다.
◦
한 노드에 연결된 모든 노드를 확인하는 연산
▪
인접 행렬의 경우, 특정 노드를 나타내는 행렬을 순회하여 연결된 노드를 가져오므로 O(N 또는 V)의 시간복잡도를 가진다.
▪
인접 리스트의 경우, 연결된 노드의 갯수가 곧 엣지의 갯수이므로 연결된 노드의 갯수만 확인하면 되므로 O(E)의 시간복잡도를 가진다.
◦
추가/삭제하는 연산
▪
추가의 경우, 인접 행렬, 리스트 모두 O(1)의 시간복잡도를 갖는다.
▪
삭제의 경우, N 또는 V의 경우, O(N+E 또는 V+E)의 시간복잡도를 갖는다. E의 경우, O(E)의 시간복잡도를 갖는다.
•
Graph 표현법은 인접성을 나타내는 것